Le filtre médian a diverses propriétés spécifiques, qui conditionnent son utilisation. Nous en donnons huit parmi les plus importantes. Pour chacune d'elles, nous ferons une comparaison avec le lissage linéaire, ce qui confirmera les points de démarcation décrits dans le document précédent. Nous concluerons sur la signification concrète du fait que le filtre médian est un opérateur morphologique plat.
L'opération de médiane choisit un de ses arguments, en fonction de la relation d'ordre entre eux. Elle se distingue ainsi de celle de la moyenne, ou de toute combinaison linéaire, qui calcule une nouvelle valeur, ce qui peut nécessiter des arrondis. Aussi quand on applique le filtre médian à une image I, la valeur de niveau de gris J(p) obtenue en un pixel p (dans la nouvelle image J) sera une des valeurs de niveaux de gris I(q) (dans l'image de départ I) d'un pixel q dans la fenêtre W(p) autour de p. Par conséquent, l'ensemble des niveaux de gris de la nouvelle image J sera inclus dans celui des niveaux de gris de l'image de départ I.
Un avantage de la non-création de niveaux de gris est qu'il ne faudra pas traiter les problèmes d'arrondi ou de précision des calculs. A partir de niveaux de gris entiers, on obtiendra des niveaux de gris entiers. De plus, il n'y aura pas d'épanchement des niveaux de gris en dehors des bornes utilisées (habituellement 0 et 255 pour les niveaux de gris). Enfin, le filtre médian peut s'appliquer aux images binaires (à valeurs 0 et 1), et le résultat restera une image binaire.
Sur ce point, le filtre médian est en total contraste avec les filtres linéaires, qui créent de nouvelles valeurs de niveaux de gris, posent des problèmes d'arrondi et dans certains cas d'épanchement de valeurs, et ne s'appliquent pas aux images binaires.
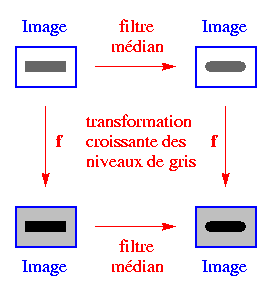
Soit f une transformation croissante des niveaux de gris appliquée à tous les pixels de l'image (par exemple, f peut être un rehaussement des niveaux de gris de l'image). Alors f commute avec le filtre médian, ce qui signifie qu'on peut :
et le résultat sera le même. C'est ce qu'indique le diagramme ci-dessous à gauche (ici f transforme le blanc en gris clair, et le gris sombre en noir).
Cela provient du fait que le choix de la médiane d'un ensemble de nombres est déterminé uniquement par la relation d'ordre entre ces nombres, et pas par les valeurs exactes qu'ils prennent. Donc si J(p) est la médiane des I(q) pour q dans W(p), alors f(J(p)) sera la médiane des f(I(q)) pour q dans W(p), parce que la relation d'ordre entre les I(q) sera préservée pour les f(I(q)).
Ainsi le filtre médian transformera les structures d'une image en fonction de leur contraste avec les structures avoisinantes, mais ce contraste n'interviendra que "qualitativement" (c.-à-d. en termes de quelle structure est plus claire ou plus sombre que les autres), et non pas "quantitativement" (c.-à-d. en raison des valeurs effectives des différences d'intensité).
Par contre, le lissage linéaire commute seulement avec une transformation linéaire des niveaux de gris.


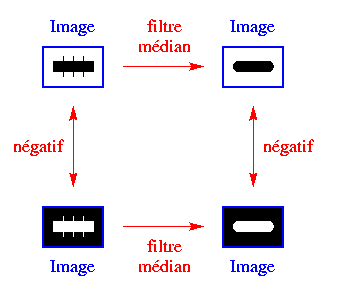
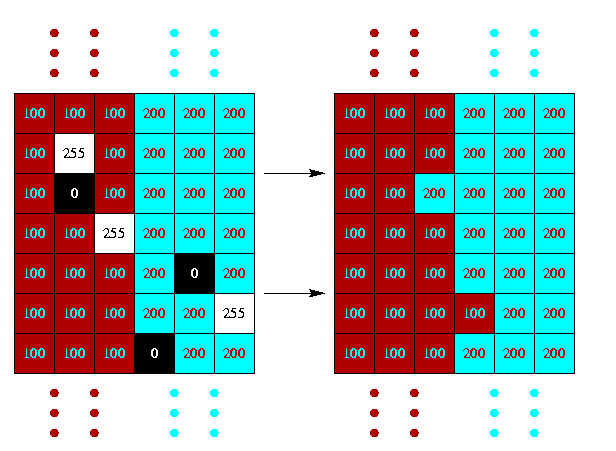
Le filtre médian est auto-dual, c.-à-d. son propre dual par inversion, en d'autres termes il commute avec l'opération de négatif (inversion de l'ordre des valeurs) dans une image. C'est ce qu'illustre le diagramme ci-dessus à droite.
En effet, si on a n valeurs numériques x1, ..., xn qui s'ordonnent de la plus petite à la plus grande xi1, ..., xin, ce qui donne la médiane xi(n+1)/2, alors comme le négatif inverse l'ordre, leurs négatifs N(x1), ..., N(xn) s'ordonneront N(xin), ..., N(xi1), ce qui donnera la médiane N(xi(n+1)/2) (si on inverse la suite ordonnée, le milieu ne change pas de position). Donc si J(p) est la médiane des I(q) pour q dans W(p), alors N(J(p)) sera la médiane des N(I(q)) pour q dans W(p).
Le lissage linéaire, qui remplace en parallèle le niveau de gris de chaque pixel par une moyenne pondérée des niveaux de gris de sa fenêtre, est aussi auto-dual. En effet, pour une image I à niveaux de gris dans un intervalle [a,b], le négatif N(I) de celle-ci sera l'image Ca+b - I, où Ca+b est l'image à valeur constante a+b. Comme la somme des coefficients du masque vaut 1, le lissage préservera Ca+b, donc
Lissage(N(I)) = Lissage(Ca+b - I) = Lissage(Ca+b) - Lissage(I) = Ca+b - Lissage(I) = N(Lissage(I)) .
L'auto-dualité du filtre médian signifie qu'ils se comportera de la même façon sur la figure et le fond (pour les images binaires), ou sur les zones claires et sombres (pour les images à niveaux de gris). De même, le lissage linéaire traitera de la même façon les zones claires et sombres d'une image à niveaux de gris. Sur ce point le filtre médian se démarque des filtres morphologiques usuels comme l'ouverture et la fermeture : l'ouverture filtre les zones claires (ou la figure), c'est le dual de la fermeture qui filtre les zones sombres (ou le fond).
Considérons n valeurs binaires x1, ..., xn, donc valant chacune 0 ou 1. Si on les ordonne de la plus petite à la plus grande, cela donnera une suite 0, ..., 0, 1, ..., 1 comprenant n0 fois 0 et n1 fois 1, où n0 + n1 = n. Comme nous supposons n impair, on a un des deux cas suivants :
Par conséquent la valeur médiane sera celle de 0 et 1 qui est majoritairement représentée parmi les n, et la médiane représente simplement un vote majoritaire parmi les valeurs.
Donc le filtre médian attribuera à chaque pixel la valeur majoritaire dans sa fenêtre. Etant donnée l'image de départ I, l'image J obtenue par filtre médian sur I se définit comme suit :
Tout ceci reste valable pour des images ayant deux niveaux de gris a0 et a1 (où a0 < a1), il suffit de remplacer ci-dessus 0 et 1 par a0 et a1. De plus, comme le filtre médian est auto-dual, l'ordre entre a0 et a1 n'a pas d'importance, il suffit d'appliquer le "vote majoritaire" dans chaque fenêtre. On peut donc appliquer le filtre médian à une image ayant deux valeurs a0 et a1 non comparables pour l'ordre, par exemple les couleurs rouge (255,0,0) et vert (0,255,0).
Comme les images binaires (à valeurs 0 et 1) correspondent aux ensembles, le filtre médian s'applique aux ensembles de pixels, ou figures. Il transformera une figure F en une nouvelle figure F' constituée de tous les pixels p tels que la majorité des pixels de W(p) sont dans la figure F.
Le filtre médian n'introduit pas de flou le long d'une arête abrupte, car celle-ci ne contient pas de dégradé, donc un tel dégradé ne pourra pas être créé. Par ailleurs, le dégradé le long d'une arête progressive ne sera pas étiré si cette arête est rectiligne. Par contre, nous verrons plus loin que le filtre médian peut étendre un dégradé présent le long d'une arête courbe ou autour d'un coin, induisant donc un effet visuel de léger flou, mais c'est sans commune mesure avec le flou provoqué par le lissage linéaire, qui introduit un dégradé.
Cette qualité provient d'une propriété du filtre médian : la préservation des marches et rampes rectilignes. Une marche représente une augmentation abrupte du niveau de gris, tandis qu'une rampe signifie une augmentation progressive et monotone du niveau de gris. Une marche ou rampe est rectiligne si l'arête qu'elle constitue dans l'image est rectiligne, en d'autres termes si le niveau de gris est à peu près constant dans la direction perpendiculaire à celle de l'augmentation. Les marches et rampes sont des modèles typiques d'arêtes dans les images ; un autre modèle est donné par la ligne, nous verrons plus loin comment le filtre médian se comporte sur celle-ci.
Nous illustrons ci-dessous le profil de niveaux de gris d'une marche et d'une rampe (dans le sens de la montée), et ensuite une marche et une rampe rectilignes où le niveau de gris augmente de bas en haut.
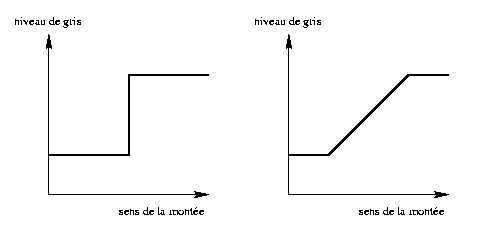 |
| Profils de niveaux de gris d'une marche (à gauche) et d'une rampe (à droite). |
 |
 |
|
| Marche rectiligne. | Rampe rectiligne. |
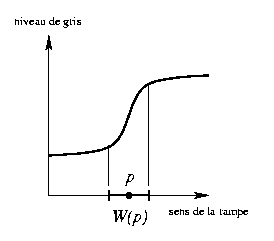
Cette propriété (de préservation des marches et rampes rectilignes) présuppose que la fenêtre W(p) correspondant au pixel p est toujours symétrique par rapport à p. Pour simplifier, considérons d'abord le cas unidimensionnel. Une marche ou une rampe donne un profil de niveaux de gris monotone croissant dans le sens de l'augmentation. Donc pour un pixel p quelconque, les niveaux de gris dans la fenêtre W(p) seront croissants, et la médiane de leurs valeurs sera celle du milieu, donc le niveau de gris du pixel au milieu de cette fenêtre W(p) ; mais nous avons supposé celle-ci symétrique par rapport à p, donc le pixel au milieu de W(p) est p, et la médiane des niveaux de gris dans W(p) est celui de p. Par conséquent, le niveau de gris d'un pixel p quelconque ne sera pas modifié par le filtre médian. Il s'ensuit qu'un profil de niveaux de gris croissant est invariant par le filtre médian à fenêtres symétriques, et c'est le cas pour les marches et rampes.
Plaçons-nous maintenant dans le cas bidimensionnel. Nous supposons les niveaux de gris monotones croissants dans un sens, et constants dans la direction perpendiculaire, comme illustré ci-dessous. On peut donner un ordre de balayage de la fenêtre W(p) autour d'un pixel p : on décompose la fenêtre en segments dans la direction selon laquelle le niveau de gris est constant (donc perpendiculaire au sens de croissance), on balaye les lignes l'une après l'autre dans le sens de croissance des niveaux de gris, et chaque ligne dans un sens donné. Dans cet ordre de balayage, les niveaux de gris des pixels croissent dans la fenêtre W(p), et la médiane de leurs valeurs sera celle du milieu, et comme la fenêtre est symétrique, cette valeur au milieu est le niveau de gris de p.
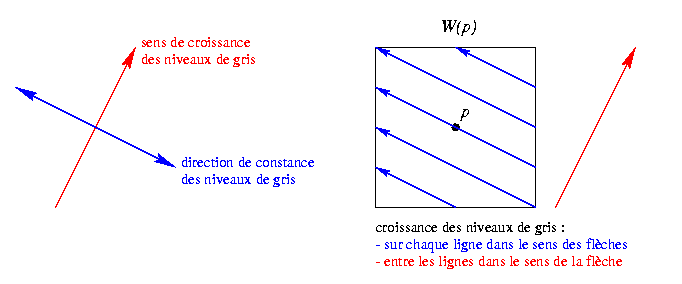
Une ligne est un profil de niveau de gris qui correspond à deux marches ou rampes successives, donc dans une direction donnée, le niveau de gris présente soit une augmentation rapide suivie d'une diminution rapide (ligne claire), soit une diminution rapide suivie d'une augmentation rapide (ligne sombre). Le comportement du filtre médian sur une ligne est de niveler cette ligne de façon à former un plateau entre l'augmentation et la diminution de niveaux de gris, de largeur (n+1)/2, où n est la largeur de la fenêtre autour d'un pixel. Si la ligne est large de moins de (n+1)/2 à sa base, elle sera entièrement effacée.
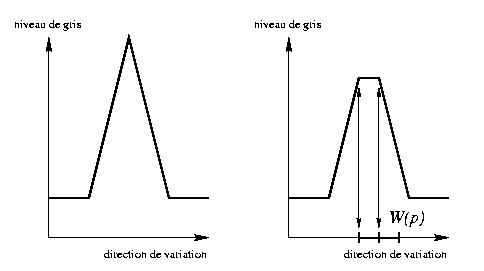
A gauche : profil de niveau de gris d'une ligne claire. A
droite : effet du filtre médian.
Du "point de vue" du filtre médian, une ligne filtrée dont le sommet forme un tel plateau, large de plus de la moitié de la taille de la fenêtre, représente une succession de deux marches ou rampes ; la fenêtre W(p) centrée autour d'un pixel p ne pourra jamais contenir à la fois une portion de la montée et une portion de la descente, elle ne peut donc "voir" que la montée ou que la descente.
Les seules arêtes préservées par le filtre médian pour toutes les tailles de fenêtre, sont les marches ou rampes rectilignes. Quand une telle arête est courbe, en prenant une taille de fenêtre suffisamment grande par rapport au rayon de courbure, le filtre médian érodera la zone convexe bordée par l'arête. C'est ce que nous illustrons ci-dessous. Le filtre médian érode uniformément un disque, ce qui revient à diminuer légèrement le diamètre de celui-ci. Par ailleurs, il arrondit les coins d'un rectangle (qui sont les points de forte courbure du bord de celui-ci), ce qui revient à réduire la courbure de l'arête aux coins. Quand le coin du rectangle présente un dégradé, celui-ci verra sa surface agrandie, ce qui peut donner une impression de léger flou. Enfin, sur un damier légèrement flou, le dégradé de gris du coin est fortement agrandi, ce qui donne un effet visuel d'accroissement du flou.
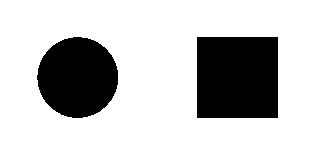 |
 |
|
| Image originale. | Résultat du filtre médian 25 × 25. | |
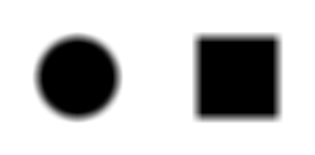 |
 |
|
| Image originale. | Résultat du filtre médian 25 × 25. | |
 |
 |
|
| Image originale. | Résultat du filtre médian 31 × 31. |
Le bruit impulsif, aussi appelé poivre et sel, est une corruption aléatoire de l'image, où chaque pixel, indépendamment l'un de l'autre, peut soit devenir très sombre ("poivre") avec une probabilité pP, soit devenir très clair ("sel") avec une probabilité pS, soit garder son niveau de gris initial avec une probabilité 1 - pP - pS. Nous allons analyser le comportement du filtre médian sur ce type de bruit, en supposant que pP, pS < 1/2.
Soit p un pixel dans une zone relativement homogène de l'image de départ I, donc les niveaux de gris des pixels de la fenêtre W(p) seront dans un intervalle étroit [a,b]. L'image est corrompue par du bruit impulsif, et soit J l'image bruitée. Posons n = |W(p)|, on a dans W(p) :
Comme pP, pS < 1/2, on peut supposer que dans la fenêtre W(p), moins de la moitié des pixels sont bruités "poivre", et moins de la moitié bruités "sel" ; donc nP < n/2 et nS < n/2. En appliquant le filtre médian à l'image bruitée J, dans la fenêtre W(p) les niveaux de gris sont ordonnés du plus petit au plus grand, ce qui donnera une suite de la forme suivante :
Comme nP < n/2, le milieu de la suite ne peut pas être dans le "poivre" ; comme nS < n/2, il ne peut pas être dans le "sel" ; par conséquent le milieu de la suite se trouvera parmi les valeurs non-bruitées, dans l'intervalle [a,b]. Ainsi, le filtre médian appliqué à l'image bruitée J donnera au pixel p un niveau de gris I(q) non-bruité (dans [a,b]) d'un pixel q de la fenêtre W(p).
En pratique, ce raisonnement peut être pris en défaut dans les deux circonstances suivantes :
Le comportement efficace du filtre médian sur le bruit impulsif est une illustration de la robustesse de la médiane par rapport aux valeurs extrêmes (outliers en anglais).
Qu'en est-il des autres types de bruit ? En théorie, le lissage linéaire élimine mieux le bruit Gaussien, mais dès que le modèle du bruit s'écarte du modèle Gaussien, le choix entre le lissage linéaire et le filtre médian est ouvert. Par ailleurs, la pondération des coefficients du lissage linéaire peut aussi revêtir une grande importance, les meilleurs résultats étant rarement obtenus avec des coefficients constants sur la fenêtre.
Nous avons vu plus haut qu'il est parfois nécessaire de répéter l'application du filtre médian pour éliminer complètement le bruit. Du point de vue algébrique, le fait qu'une deuxième application du filtre médian peut encore modifier une image signifie qu'en tant qu'opérateur sur les images, le filtre médian n'est pas idempotent. Se pose alors la question suivante : si on répète l'application du filtre médian sur une image, finira-t-on par aboutir sur une image qui ne sera plus modifiée par une application ultérieure du filtre ? Une telle image serait considérée comme "parfaitement filtrée". Le résultat suivant a été démontré :
Soit I une image dont les valeurs sont constantes en dehors d'un support borné. Considérons le filtre médian avec des fenêtres symétriques. Alors l'application répétée du filtre sur I aboutira après un nombre fini de fois à un image J vérifiant l'une des deux conditions suivantes :
En d'autres termes, le filtre médian finit par aboutir soit à une image fixe, soit à une oscillation entre 2 images. Nous donnons ci-dessous un exemple, dû à Goles et Olivos (1981), avec la fenêtre W(p) de 5 pixels en forme de + (formée de p et de ses 4 voisins axiaux), d'une oscillation entre deux figures (images binaires) A and B :
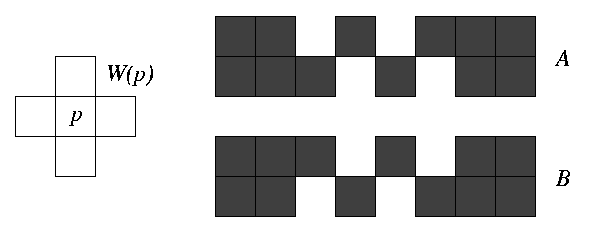
Dans le cas d'une image non bornée, il y a des exemples bien connus d'une image oscillant avec son négatif sous l'effet du filtre médian :
Le filtre médian est un opérateur morphologique plat, dérivé de l'opérateur ensembliste appliquant le "vote majoritaire" dans chaque fenêtre. Cela signifie qu'il traite une image à niveaux de gris comme un empilement d'images binaires, qu'il filtrera chacune séparément, pour les empiler à nouveau. Les opérateurs morphologiques plats (par exemple : la dilatation, l'érosion, l'ouverture ou la fermeture d'une image à niveaux de gris par un élément structurant ensembliste) partagent avec le filtre médian les propriétés suivantes :