 X, et pour tout
pixel q, d(p,X)
X, et pour tout
pixel q, d(p,X)  d(p,q) +
d(q,X).
d(p,q) +
d(q,X).
Soit d une distance (euclidienne ou de chanfrein) sur le plan discret Z2. Etant donnés un pixel p et un ensemble X de pixels de Z2, pour un rayon r > 0, il n'y a qu'un nombre fini de pixels x de X tels que d(p,x) < r, donc en prenant parmi ceux-ci le plus proche de p, on obtient un pixel x de X à distance minimum de p. On définit ainsi la distance d(p,X) de p à X comme le minimum de la distance de p aux pixels de X :
d(p,X) = min {d(p,x) | x dans X}.
On a d(p,X) = 0 si et seulement si
p  X, et pour tout
pixel q, d(p,X)
X, et pour tout
pixel q, d(p,X)  d(p,q) +
d(q,X).
d(p,q) +
d(q,X).
Soient S une partie de Z2 et R une partie de S. La transformée de distance de R dans S est la fonction TFDR,S définie sur S et à valeurs non-négatives, donnée par :
TFDR,S(p) = d(p,R) pour tout pixel p de S.
L'ensemble R est appelé marqueur, tandis que l'ensemble S est appelé domaine ou masque. Notons que certains auteurs définissent la transformée de distance de R comme la fonction associant à tout pixel p sa distance au complémentaire S \ R de R dans S.
L'approche naïve pour calculer la transformée de distance serait d'évaluer d(p,q) pour tout p dans S et tout q dans R, et d'en déduire d(p,R), ce qui donnerait une complexité proportionnelle à |S| × |R|. Lorsque le domaine est une grille rectangulaire et la distance est une distance de chanfrein satisfaisant les conditions de Montanari, il existe un algorithme séquentiel calculant la transformée de distance au terme de deux balayages du domaine. Sa complexité est proportionnelle à |S| × m, où m est la taille du masque de chanfrein. Il s'appuie sur deux concepts, l'ordre de balayage de la grille formant le domaine, et la décomposition du masque de chanfrein en masque antérieur et masque postérieur.
Dans un algorithme séquentiel, les pixels de la grille sont visités l'un après l'autre dans un certain ordre, appelé ordre de balayage. On dira que p est antérieur à q, et on notera p < q, si p est visité avant q dans le balayage. Donc les pixels sont balayés du premier au dernier. A cet ordre correspond l'ordre de balayage inverse >, où les pixels sont balayés du dernier au premier.
L'ordre de balayage ne peut pas être arbitraire, il doit respecter la contrainte de régularité : si p < q, alors pour tout pixel x on a p + x < q + x, ce qui signifie que le fait que p < q ne dépend que de l'orientation du vecteur pq. L'ordre lexicographique donné par
(i,j) < (i',j') ssi i < i' ou [i = i' et j < j'],
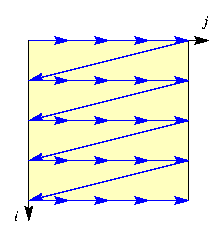
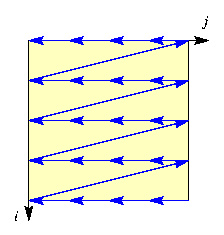
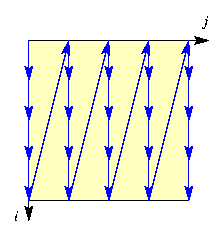
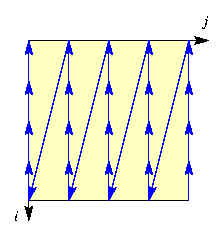
est régulier, il correspond au balayage de la première ligne à la dernière, et au sein de chaque ligne de la première colonne à la dernière. L'ordre lexicographique inverse, correspondant au balayage de la dernière ligne à la première, et au sein de chaque ligne de la dernière colonne à la première, est également régulier. Le sont aussi l'ordre lexicographique transposé, où la priorité entre lignes et colonnes est inversée (on balaie de la première colonne à la dernière, et au sein de chaque colonne, de la première ligne à la dernière), et l'ordre lexicographique transposé inverse (de la dernière colonne à la première, et au sein de chaque colonne, de la dernière ligne à la première).
Le tableau ci-dessous illustre le balayage correspondant à chacun de ces ordres, ainsi que la double boucle d'itération sur les coordonnées (i,j) réalisant ce balayage :
| ordre lexicographique | ordre lexicographique inverse | |
 |
 |
|
| pour i allant du premier au dernier
faire pour j allant du premier au dernier faire |
pour i allant du dernier au premier
faire pour j allant du dernier au premier faire |
| ordre lexicographique transposé | ordre lexicographique transposé inverse | |
 |
 |
|
| pour j allant du premier au dernier
faire pour i allant du premier au dernier faire |
pour j allant du dernier au premier
faire pour i allant du dernier au premier faire |
A partir de maintenant, nous choisissons l'ordre lexicographique, mais ce qui suit peut s'adapter aux autres ordres.
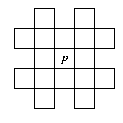
Pour tout pixel p, soit V(p) le voisinage de p sur lequel est défini le masque de chanfrein (NB. V(p) contient p). Donc V(p) est formé de p et des ses 4-voisins pour d4, de p et des ses 8-voisins pour d8 ou pour toute autre distance de chanfrein 3 × 3 (comme la distance (3,4) de Borgefors) ; pour une distance de chanfrein 5 × 5 (comme la distance (5,7,11) de Borgefors), V(p) est le voisinage de p de taille 17 illustré ci-contre. Soit Mp le masque de chanfrein positionné en p ; donc Mp est une fonction définie sur V(p) et à valeurs non-négatives, telle que pour tout q dans V(p), la valeur Mp(q) du masque de chanfrein en q définit la distance de q à p.
Nous définissons le voisinage antérieur de p comme l'ensemble V¯(p) des pixels de V(p) qui sont antérieurs ou égaux à p dans l'ordre de balayage, ainsi que le voisinage postérieur de p comme l'ensemble V+(p) des pixels de V(p) qui sont postérieurs ou égaux à p dans l'ordre de balayage :
V¯(p) = {q dans V(p) | q
p}, et
V+(p) = {q dans V(p) | qp}
Le masque de chanfrein antérieur en p est la restriction M¯p du masque de chanfrein Mp au voisinage antérieur V¯(p) ; de même, le masque de chanfrein postérieur en p est la restriction M+p du masque de chanfrein Mp au voisinage postérieur V+(p). Nous illustrons ci-dessous les masques Mp, M¯p et M+p, pour les distances d4, d3,4 et d5,7,11 dans le cas de l'ordre lexicographique :
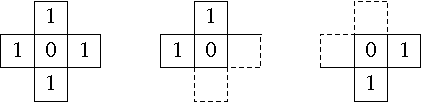
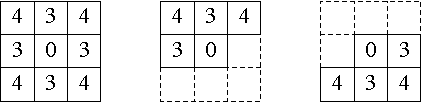
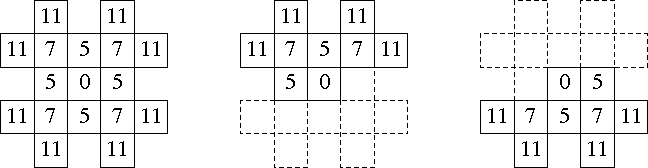
Nous pouvons maintenant dérire l'algorithme séquentiel de transformée de distance. Il comporte trois étapes : une initialisation, un premier balayage dans l'ordre direct, et un deuxième dans l'ordre inverse.
f est une fonction définie sur S.
H est un nombre considéré comme "infini".0) Initialisation
Pour chaque p dans S on pose
f(p) := 0 si p
R,
f(p) := H si pS\R.
1) Balayage dans l'ordre direct :
Pour le pixel p allant du premier au dernier, faire
f(p) := min { f(q) + M¯p(q) | q dans V¯(p) }.
2) Balayage dans l'ordre inverse :
Pour le pixel p allant du dernier au premier, faire
f(p) := min { f(q) + M+p(q) | q dans V+(p) }.
On a TFDR,S(p) = f(p).
Cet algorithme appelle trois remarques :
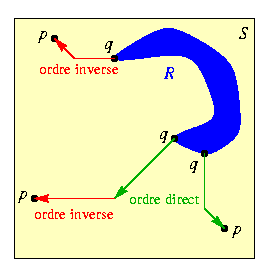
Expliquons brièvement pourquoi cet algorithme est correct. Soit p un pixel de S, et soit q le pixel de R le plus proche de p. Comme la distance de chanfrein satisfait les conditions de Montanari, tout chemin de poids minimum de q à p emprunte au plus deux directions, et on peut arbitrairement choisir l'ordre dans lequel sont combinés les déplacements selon chacune des deux directions. Si le chemin emprunte une seule direction, ou deux directions orientées toutes deux vers l'avant ou toutes deux vers l'arrière (pour l'ordre de balayage), on combine ces déplacements dans n'importe quel ordre. Au cas où le chemin utilise deux directions dont l'une va vers l'avant et l'autre vers l'arrière (pour l'ordre de balayage), on choisira un chemin empruntant d'abord la direction vers l'avant, et ensuite celle vers l'arrière (cfr. la figure ci-contre). Comme S est rectangulaire, ce chemin sera entièrement inclus dans S. Lors de l'initialisation, le pixel q obtient la valeur correcte pour TFDR,S. Au cours du premier balayage dans l'ordre direct, les pixels sur le tronçon de chemin vers l'avant obtiennent l'un après l'autre la valeur correcte pour TFDR,S. Au cours du second balayage dans l'ordre inverse, les pixels sur le tronçon de chemin vers l'arrière obtiennent l'un après l'autre la valeur correcte pour TFDR,S.
Notons que l'algorithme décrit ci-dessus ne garantit pas un résultat correct pour une distance de chanfrein qui ne satisferait pas les conditions de Montanari (comme par exemple la distance induite par les mouvements du cavalier sur l'échiquier), les chemins de poids minimum pouvant sortir hors de la grille. Par ailleurs cet algorithme ne peut pas s'adapter au calcul de la transformée de distance euclidienne. En effet, quand le marqueur R est concave, pour tout pixel p du domaine S, le pixel q du marqueur R à distance euclidienne minimum de p n'est pas nécessairement celui à distance minimum d'un des pixels voisins de p