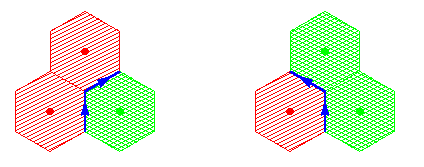
On considère le maillage carré du plan. Soient F la figure, B = Z2 \ F le fond, k le nombre désignant l'adjacence choisie sur F (k = 4 ou 8), et k' celui désignant l'adjacence opposée sur B (donc k' = 12 - k, c.-à-d. {k,k'} = {4,8}).
Nous supposons la figure F bornée. On peut donc limiter le plan discret Z2 à une grille (matrice) rectangulaire
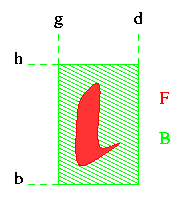
G = {h, ..., b} × {g, ..., d},
contenant la figure F, et telle que tous les pixels sur le pourtour de la grille (les lignes h et b et les colonnes g et d) appartiennent au fond B (donc la figure est strictement à l'intérieur de la grille).

Soit X une composante k-connexe de F, et Y une composante k'-connexe de B. Supposons que X soit 8-adjacente à Y, c.-à-d. il y a un pixel x de X 8-adjacent à un pixel y de Y. Si x n'est pas 4-adjacent à y (donc ils sont diagonalement adjacents), considérons un pixel z 4-adjacent à la fois à x et à y. Si z appartient à F, comme il est 4-adjacent au pixel x de X, il appartiendra à X ; donc le pixel z de X sera 4-adjacent au pixel y de Y. De même si z appartient à B, alors il appartiendra à Y, et le pixel x de X sera 4-adjacent au pixel z de Y. Par conséquent X est 4-adjacente à Y. Les trois cas sont illustrés ci-dessous.
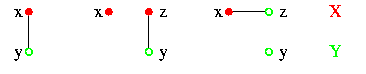
Donc une composante k-connexe X de F et une composante k'-connexe Y de B sont 8-adjacentes si et seulement si elles sont 4-adjacentes. On dira donc simplement qu'elles sont adjacentes.
Soient x un pixel de la figure, et y un pixel du fond, qui sont 4-adjacents. Les cellules carrées C(x) et C(y) s'intersectent en un segment fermé (contenant ses extrémités), qui constitue l'élément d'arête euclidien entre ces deux pixels. La représentation discrète de cet élément d'arête se fera par le point médian de ce segment, en d'autres termes le point situé au milieu entre x et y. Ce point a une coordonée entière, l'autre entière plus un demi. Nous illustrons ci-dessous les représentations discrète (à gauche) et euclidienne (à droite) de cet élément d'arête (la figure en rouge, le fond en vert, et l'arête en bleu) :
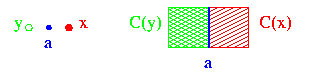
Etant données une composante k-connexe X de la figure et une composante k'-connexe Y du fond, adjacente à X, on définit l'arête entre X et Y comme l'ensemble des éléments d'arête entre pixels 4-adjacents de X et Y, comme illustré ci-dessous, en représentation discrète (à gauche) et euclidienne (à droite) :
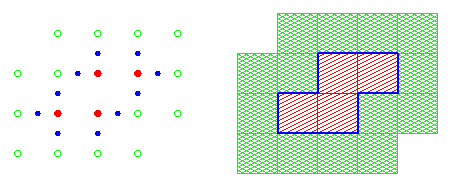
Comme on le voit dans la représentation euclidienne, ces éléments d'arête s'enchaînent en cycles. Comme la figure est bornée, ces cycles sont finis, et se trouvent en fait à l'intérieur de la grille G. On peut orienter les éléments d'arête de façon à donner un sens de parcours pour ces cycles. Comme nous l'illustrons ci-dessous, il y a deux choix pour cette orientation des éléments d'arête, à savoir celle laissant la figure à gauche et le fond à droite (illustrée à gauche), et celle laissant la figure à droite et le fond à gauche (illustrée à droite) :
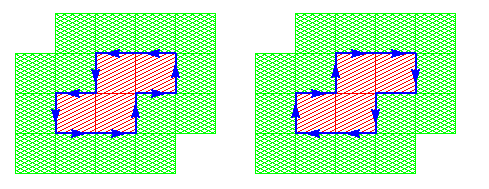
Etant donné un choix d'orientation, on peut déterminer pour tout élément d'arête a son unique successeur dans le cycle ; pour cela il suffit d'examiner l'appartenance à la figure ou au fond des deux pixels x et y situés de part et d'autre de la prolongation en ligne droite de cet élément d'arête, comme illustré ci-dessous dans le cas du choix d'orientation laissant la figure à gauche :
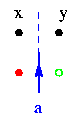
Comme le pourtour de la grille G ne contient pas de pixels de la figure, x et y ne peuvent pas se trouver en dehors de cette grille. Dans trois cas la détermination du successeur de l'élément d'arête est évidente :
Dans le quatrième cas, celui où l'on a un carré de pixels, avec deux pixels de la figure diagonalement adjacents et deux pixels du fond diagonalement adjacents, il y a indétermination pour le successeur de l'élément d'arête :
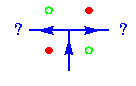
Ici la détermination du successeur dépend du choix de l'adjacence pour la figure et le fond. Si on reprend l'argumentation sur les connexités opposées sur la figure et le fond, on associe à chaque pixel une cellule, et les bords des cellules à la frontière entre la figure et le fond correspondent à la figure pour k = 4, et au fond pour k = 8. On voit alors que pour k = 4 il y a un tournant à gauche, et pour k = 8 un tournant à droite :
Donc tout élément d'arête a un unique successeur. De même il a un unique prédécesseur (en fait, son unique successeur pour l'orientation opposée), et ainsi ces éléments d'arêtes s'enchaînent en cycles, qui peuvent être suivis grâce à la méthode vue ci-dessus.
Notons que dans le maillage triangulaire correspondant aux pixels hexagonaux, le suivi d'arêtes est beaucoup plus simple, car pour la détermination du successeur d'un élément d'arête, il n'y a que deux cas à considérer :