 512 × 512 |
||
 256 × 256 |
 128 × 128 |
 64 × 64 |
Un appareillage optique (lentille, miroir, etc.) peut disperser les rayons lumineux, ce qui diminue la netteté des images ainsi produites, par exemple en créant du flou. En optique, on appelle la résolution d'un appareillage, la distance minimum entre deux sources lumineuses ponctuelles permettant de les distinguer. Plus cette distance est petite, mieux on voit les détails de l'image ainsi produite ; on dit que la résolution est plus fine ou plus grossière selon que cette distance est plus petite ou plus grande.
En imagerie informatique (écran d'ordinateur, appareil photo numérique, imprimante, numérisateur "scanner", etc.), une image est formée par un alignement horizontal et vertical de points lumineux appelés pixels. Pour que deux sources ponctuelles lumineuses apparaissent distinctement dans une telle image, ils faut qu'elles soient sur deux pixels distincts, ou mieux, sur deux pixels séparés par au moins un pixel. Par conséquent la résolution, au sens optique, d'un système d'imagerie informatique, se mesure par les dimensions spatiales d'un pixel. La résolution est plus fine ou plus grossière selon que les dimensions des pixels sont plus petites ou plus grandes. Généralement, la largeur et la hauteur d'un pixel sont égales (un pixel est carré), donc on peut mesurer la résolution par le nombre de pixels par unité de longueur.
Pour une imprimante, ainsi que pour un numérisateur, on mesure la résolution en dpi, qui est l'abbréviation de l'anglais dots per inch, c.-à-d. le nombre de pixels par pouce (environ 2,54 cm). Donc une résolution de 300 dpi est deux fois plus fine qu'une de 150 dpi, parce que les dimensions (hauteur, largeur) d'un pixel seront deux fois plus petites. De même, pour un appareil photo numérique, la résolution sera donnée par le nombre de pixels en largeur et en hauteur dans une photo.
Lorsque la résolution est deux fois plus fine, il y a deux fois plus de pixels à la fois en largeur et en hauteur, donc la taille informatique de l'image (nombre de pixels) sera multipliée par quatre ; plus généralement, une résolution n fois plus fine donne une image n2 fois plus volumineuse.
Sur un écran d'ordinateur, la taille des pixels, donc la résolution, est fixée une fois pour toute ; par exemple un écran dont les dimensions sont de rapport H/L = 4/5 pourra avoir 1024 pixels en hauteur et 1280 en largeur. Une image numérisée à résolution plus fine apparaîtra tout simplement plus grande sur l'écran.
Pour obtenir à partir d'une photo donnée une image plus petite, soit on numérise la photo avec une résolution plus grossière, soit on réduit la grande image par un procédé informatique. Pour une résolution n fois plus grossière (c.-à-d. une image informatique avec n fois moins de pixels en largeur et en hauteur), un pixel correspondra à un carré n × n de pixels dans l'image à résolution fine (volumineuse). D'ailleurs le procédé informatique le plus commun pour réduire une image consiste à la diviser en blocs carrés n × n et calculer sur chaque bloc la moyenne des intensités, ainsi cette intensité moyenne sera celle du pixel correspondant dans l'image réduite. Il existe cependant des méthodes de réduction plus élaborées, où l'intensité d'un pixel réduit sera la moyenne pondérée de celles sur une fenêtre autre que le carré n × n.
Nous montrons ci-dessous une image (Lenna, © Playboy), à des tailles (en pixels) successives de 512 × 512, 256 × 256, 128 × 128, et 64 × 64.
 512 × 512 |
||
 256 × 256 |
 128 × 128 |
 64 × 64 |
Une image de dimensions n fois plus petites peut être ramenée à la taille originelle par un procédé informatique d'agrandissement, remplaçant chaque pixel par un carré n × n de pixels ayant tous la même intensité. Cela donne ainsi le même effet que si l'image était affichée avec des pixels n fois plus grands, c.-à-d. comme si l'écran avait une résolution n fois plus grossière.
Ce procédé d'agrandissement, où un pixel donne lieu à un carré de pixels de même intensité, repose sur ce qu'on appelle l'interpolation au plus proche voisin (les pixels nouvellement créés prennent la valeur de leur plus proche voisin). Il y a d'autres techniques où le carré de pixels correspondant à un pixel de l'image réduite prend des intensités variant linéairement dans chaque direction, sans discontinuité entre deux carrés voisins (on fait alors une interpolation bilinéaire). On peut aussi utiliser des splines pour avoir une transition lisse de niveaux de gris d'un carré au carré voisin.
Nous montrons ci-dessous l'image réduite d'un facteur 2, ramenée à la taille originelle ; la résolution est ainsi 2 fois plus grossière, puisque les pixels sont en fait des carrés 2 × 2 de pixels. On voit apparaître un effet de crénelage des contours dans les directions obliques : la ligne de contour, au lieu d'apparaître lisse, prendra la forme d'un escalier. Par ailleurs, des détails très fins (comme les cils) sont brouillés.

Image 256 × 256 agrandie
à 512 × 512 (facteur 2)
Cet effet de crénelage des lignes peut parfois induire des impressions visuelles de texture, c'est un défaut inévitable de la numérisation quand la résolution est plus grossière que celle de l'oeil humain.
Nous montrons ensuite les images réduites par des facteurs 4 et 8, et ramenées à la taille originelle (donc de résolution 4 et 8 fois plus grossière). Avec le facteur 4, l'effet de crénelage des contours et de brouillage des détails devient très prononcé. Avec le facteur 8, on obtient un effet de "pixelisation", de nombreux détails sont méconnaissables.
Ces effets de crénelage de contours et de "pixellisation" peuvent être atténués si on applique dans chaque carré n × n une interpolation bilinéaire ou par splines. Il existe également des techniques spécifiques de traitement d'images permettant d'atténuer ces effets dans une image de résolution trop grossière. Elles reposent essentiellement sur un lissage. Cependant on ne peut généralement pas compenser la perte de détails due à la résolution plus grossière.

Image 128 × 128 agrandie
à 512 × 512 (facteur 4)

Image 64 × 64 agrandie
à 512 × 512 (facteur 8)
La couleur d'un pixel sur un écran est obtenue par une combinaison de trois rayons rouge, vert et bleu d'intensités variables. Ainsi la couleur est codée par 3 nombres correspondant à ces intensités, et généralement ces nombres seront des entiers entre 0 et 255, ce qui permet de coder la couleur avec 3 octets (1 octet pour chacune des composantes rouge, verte, et bleue). Pour une image à niveaux de gris, les rayons rouge, vert et bleu auront une intensité égale, aussi on ne code qu'un nombre, correspondant à la luminance ; on utilisera donc un octet pour coder celle-ci, puisqu'elle correspondra à un entier entre 0 et 255.
Si pour coder l'intensité (luminance, ou composantes rouge / verte /bleue) on avait utilisé, au lieu d'un octet, un nombre de bits m < 8, on aurait 2m valeurs différentes d'intensité, au lieu de 256. Donc on verrait moins de nuances de couleurs ou de niveaux de gris. Combien de niveaux d'intensité sont nécessaires ? Nous montrons ci-dessous une image à 256 niveaux de gris, affichée successivement avec 256, 128, 64, 32, 16, 8, 4 et 2 niveaux de gris, c.-à-d. 2m pour m descendant de 8 à 1. En fait, l'image à 2m valeurs de niveaux de gris a ses niveaux de gris affichés dans l'intervalle de 0 à 255, mais ceux-ci varient par pas de 255 / (2m - 1), ce qui fait 2m valeurs allant de 0 à 255.
 256 niveaux de gris (m = 8) |
 128 niveaux de gris (m = 7) |
 64 niveaux de gris (m = 6) |
 32 niveaux de gris (m = 5) |
 16 niveaux de gris (m = 4) |
 8 niveaux de gris (m = 3) |
 4 niveaux de gris (m = 2) |
 2 niveaux de gris (m = 1) |
L'interprétation de ces images successives doit tenir compte de la qualité du support (écran, impression) sur lequel elles apparaissent. Par exemple certaines imprimantes ont une gamme de niveaux de gris limitée à 32, et un bon nombre de navigateurs web n'affichent correctement qu'un nombre limité de couleurs et de niveaux de gris. En supposant une qualité optimale du support, l'oeil humain ne distingue pratiquement pas de différence entre 256 et 128 niveaux de gris. Ensuite, apparaît peu à peu le phénomène de faux contours : un dégradé progressif dans les intensités prendra la forme d'une montée par paliers, donc on verra, à la place de ce dégradé, différentes bandes homogènes séparées par des contours. Cela apparaît très fortement dans l'image à 16 niveaux de gris. Enfin, en dessous de 8 niveaux de gris, l'image est méconnaissable ; l'intérêt d'un nombre aussi faible de niveaux de gris ne peut être qu'artistique.
Une image de taille H × L ayant ses valeurs (niveaux de gris ou couleurs) dans une gamme de taille 2m, nécessite HLm bits. Donc le volume qu'elle occupe est proportionnel au carré de la résolution et au logarithme de la taille de la gamme de couleurs ou niveaux de gris. Se pose alors la question : vaut-il mieux augmenter la résolution, ou la taille de la gamme de valeurs ? D'après les expériences menées par Huang en 1965 sur des images en niveaux de gris, il ressort que la réponse dépend du type d'image ; on peut classer les images en 3 catégories, selon leur niveau de détail :
On trouvera ci-dessous un exemple d'image de chaque catégorie: un visage (bas niveau de détail), un personnage dans une scène (niveau moyen de détail), et une foule (haut niveau de détail).
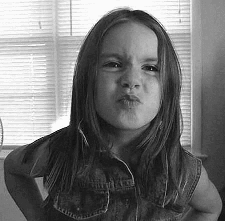 grandes régions, bas niveau de détail |
 régions moyennes, niveau moyen de détail |
|
 petites régions, haut niveau de détail |
||
Pour toutes les images, la qualité visuelle augmente avec la résolution. En ce qui concerne le nombre de niveaux de gris, cela dépend du type d'image. Pour une image à haut niveau de détail, le nombre de niveaux de gris importe peu ; en effet, il n'est pas nécessaire de voir des dégradés, seul compte le contraste entre petites régions bien identifiées. Par contre, pour une image à bas niveau de détail, la qualité visuelle augmente avec le nombre de niveaux de gris, mais pas vraiment au-delà de 32 ou 64.