L'égalisation d'histogramme est une méthode radicale de rehaussement, qui impose sur l'image une répartition la plus homogène possible des niveaux de gris. Cependant dans la plupart des situations concrètes, on recherche une image ayant un bon contraste entre les objets et le fond, et entre les différentes parties d'un objet, aussi l'égalisation ne donne pas le résultat escompté (voir en particulier l'image égalisée dans le document précédent).
Une alternative est de spécifier au départ la répartition souhaitée des niveaux de gris dans l'image, donc de se donner un histogramme qu'on voudrait obtenir grâce à une transformation croissante des niveaux de gris de l'image. La question se pose alors de savoir comment calculer cette transformation des niveaux de gris.
La solution à cette question peut être donnée dans le cadre du cas continu, qui avait permis d'obtenir la formule d'égalisation. Soit I l'image de départ et HI son histogramme. Soit HS l'histogramme spécifié que l'on souhaite obtenir. Il faut obtenir une fonction f croissante des niveaux de gris tel que l'image J définie par J(p) = f(I(p)) ait l'histogramme HS. Le calcul utilisé dans le cas de l'histogramme plat ne peut pas se généraliser, aussi nous utiliserons un autre raisonnement.
On suppose qu'on a obtenu une telle fonction f qui, appliquée à l'image I, donne l'image J = f o I d'histogramme HS. Supposons qu'on égalise chacune des deux images I et J par les fonctions croissantes de niveaux de gris fI et fJ respectivement. Donc les deux images
| fI o I | définie par | (fI o I)(p) = fI(I(p)) | |
| et | fJ o J = fJ o f o I | définie par | (fJ o J)(p) = fJ(J(p)) = fJ(f(I(p))) = (fJ o f o I)(p) |
ont un histogramme plat. De plus, elles sont toutes deux obtenues à partir de I en y appliquant respectivement les deux fonctions croissantes de rehaussement fI et fJ o f. Or le calcul donné pour l'égalisation d'histogramme montre que celle-ci ne peut être obtenue que d'une seule façon par une fonction croissante de niveaux de gris. On en conclut que
fI = fJ o f et ainsi f = fJ-1 o fI.
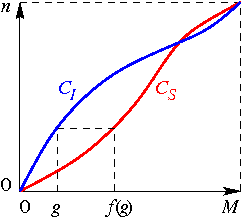
Il suffit donc d'appliquer la fonction fJ-1 o fI aux niveaux de gris de I. Notons que les fonctions fI et fJ sont construites uniquement à partir des histogrammes HI et HS, sans qu'il soit nécessaire de connaître l'image J. En effet, on en dérive les histogrammes cumulatifs CI et CS, et alors pour tout niveau de gris g on a
fI(g) = M CI(g) / n et fJ(g) = M CS(g) / n,
et ainsi f(g) = fJ-1(fI(g)) = h tel que CS(h) = CI(g), comme illustré ci-dessous :

Le problème principal est l'inversion de la fonction fJ (ou CS). Celle-ci est croissante, mais généralement pas bijective. Dans le cas continu elle est surjective, mais pas nécessairement injective ; plus précisément, elle est strictement croissante (donc injective) sur les zones de niveaux de gris g avec HS(g) > 0, mais constante sur les zones de niveaux de gris g avec HS(g) = 0. Dans le cas discret, les effets d'arrondi font qu'elle sera presque toujours ni surjective ni injective. La figure ci-dessous représente la situation où on a un niveau de gris g tel que fI(g) ne soit pas dans l'image de fJ, mais intermédiaire entre deux éléments successifs h et h' de l'image de fJ, et que ces deux niveaux de gris aient pour image inverse par fJ les intervalles [a,b] et [b+1,c] respectivement.
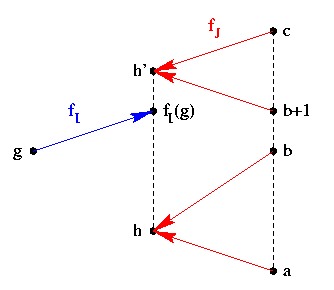
Ici, pour attribuer une valeur à (fJ-1 o fI)(g) = fJ-1(fI(g)), on doit choisir une valeur dans l'intervalle [a,c]. On peut par exemple poser
fJ-1(h) = (a + b)/2 et fJ-1(h') = (b + 1 +c)/2,
et par interpolation linéaire on obtient ainsi
fJ-1(fI(g)) = (a + b)/2 + (fI(g) - h) (c + 1 - a) / 2(h' - h).